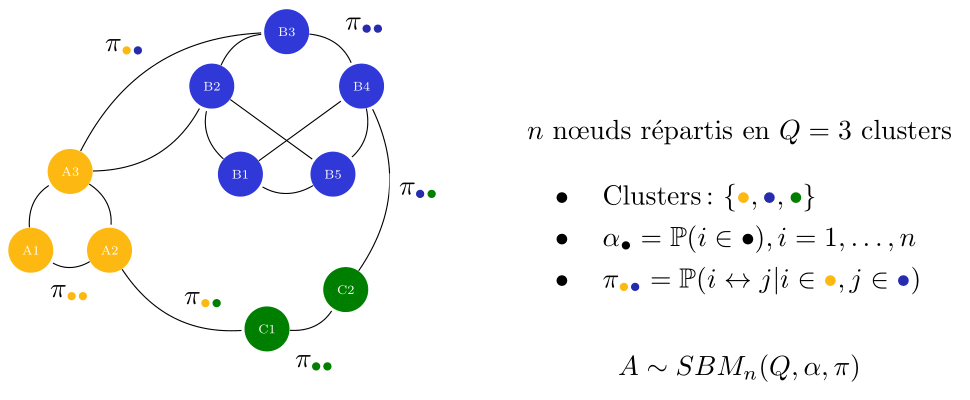
Stochastic block model

Probabilistic model of network, credits to Sophie Donnet and Pierre Barbillon

\documentclass[varwidth,border=3pt,tikz]{standalone}
\usepackage{multicol}
\usepackage{tikz}
\usepackage{amsmath}
\usepackage{amssymb}
\usepackage{enumitem}
%\usetikzlibrary{calc,shapes,backgrounds,arrows,automata,shadows,positioning}
\usetikzlibrary{arrows,shapes,positioning,shadows,trees,calc,backgrounds,automata,positioning}

\tikzset{
  basic/.style  = {draw, text width=3cm, font=\sffamily, rectangle},
  root/.style   = {basic, rounded corners=2pt, thin, align=center,
                   fill=green!30},
  level 2/.style = {basic, rounded corners=6pt, thin,align=center, fill=green!60,
                   text width=8em},
  level 3/.style = {basic, thin, align=left, fill=pink!60, text width=3.5cm}
}

% pour tickz multilevel
\definecolor{redorg}{RGB}{215,48,39}
\definecolor{orangeorg}{RGB}{253,174,97}
\definecolor{blueind}{RGB}{69,117,233}
\definecolor{cyanind}{RGB}{116,173,209}
\definecolor{greenind}{RGB}{112,130,56}
\definecolor{dgreen2}{RGB}{48,56,215}

\begin{document}


        \begin{tikzpicture}
          %% UN GRAPH
      \tikzstyle{every edge}=[-,>=stealth',shorten >=1pt,auto,thin,draw]
      \tikzstyle{every state}=[draw=none,text=white,scale=0.65, font=\scriptsize, transform shape]
      \tikzstyle{every node}=[fill=yellow!40!orange]
      % premier cluster
      \node[state] (A1) at (0,0.5) {A1};
      \node[state] (A2) at (1,0.5) {A2};
      \node[state] (A3) at (.5,1.5) {A3};

      \path (A2) edge [bend left] node[fill=white,below=.1cm]
      {$\pi_{\textcolor{yellow!40!orange}{\bullet}\textcolor{yellow!40!orange}{\bullet}}$}
      (A1)
      (A1) edge [bend left] (A3)
      (A3) edge [bend left] (A2);

      \tikzstyle{every node}=[fill=dgreen2!80!black]
      \foreach \angle/\text in {234/B1, 162/B2, 90/B3, 18/B4, -54/B5} {
        \node[fill=dgreen2,state,xshift=5cm,yshift=3.5cm]     (\text)    at
        (\angle:1cm) {\text};
      }
      \path (B2) edge (B5)
      (B1) edge (B4);
      \foreach \from/\to in {1/2,2/3,4/5,5/1}{
        \path (B\from) edge [bend left] (B\to);
      }

      \path    (B3)    edge     [bend    left]    node[fill=white]
      {$\pi_{\textcolor{dgreen2!80!black}{\bullet}\textcolor{dgreen2!80!black}{\bullet}}$}  (B4) ;
      
      \tikzstyle{every node}=[fill=green!50!black]
      % troisieme cluster
      \node[state] (C1) at (3,-.5) {C1};
      \node[state] (C2) at (4,0) {C2};

      \path (C1) edge [bend right] node[fill=white,below=.25cm]
      {$\pi_{\textcolor{green!50!black}{\bullet}\textcolor{green!50!black}{\bullet}}$}
      (C2);

      % inter cluster
      \path (A3) edge [bend right]  (B2)
      (A3)    edge    [bend    left]    node[fill=white]
      {$\pi_{\textcolor{yellow!40!orange}{\bullet}\textcolor{dgreen2!80!black}{\bullet}}$}
      (B3)
      (C2) edge [bend right] node[fill=white,right]
      {$\pi_{\textcolor{dgreen2!80!black}{\bullet}\textcolor{green!50!black}{\bullet}}$}
      (B4)
      (A2) edge [bend right] node[fill=white]
      {$\pi_{\textcolor{yellow!40!orange}{\bullet}\textcolor{green!50!black}{\bullet}}$}
      (C1);
      
      \tikzstyle{every node}=[fill=white]

      \node at (9,2) {$n$ nœuds répartis en $Q=3$ clusters};

      \node[below=1,align=center ] at (9,2.5) {$\begin{aligned}
        & \bullet \quad \text{Clusters\,:}\  \{\textcolor{yellow!40!orange}{\bullet},\textcolor{dgreen2!80!black}{\bullet},\textcolor{green!50!black}{\bullet}\}\\
     & \bullet \quad \alpha_{\bullet}  =  \mathbb{P}(i  \in  \bullet), i=1,\dots,n \\
     & \bullet \quad \pi_{\textcolor{yellow!40!orange}{\bullet}\textcolor{dgreen2!80!black}{\bullet}}     =      \mathbb{P}(i
     \leftrightarrow j | i\in\textcolor{yellow!40!orange}{\bullet},j\in\textcolor{dgreen2!80!black}{\bullet})
     \end{aligned}$
     };
     
     \node at (9,-1) {$A \sim SBM_{n}(Q,\alpha,\pi)$};

   

  \end{tikzpicture}


\end{document}