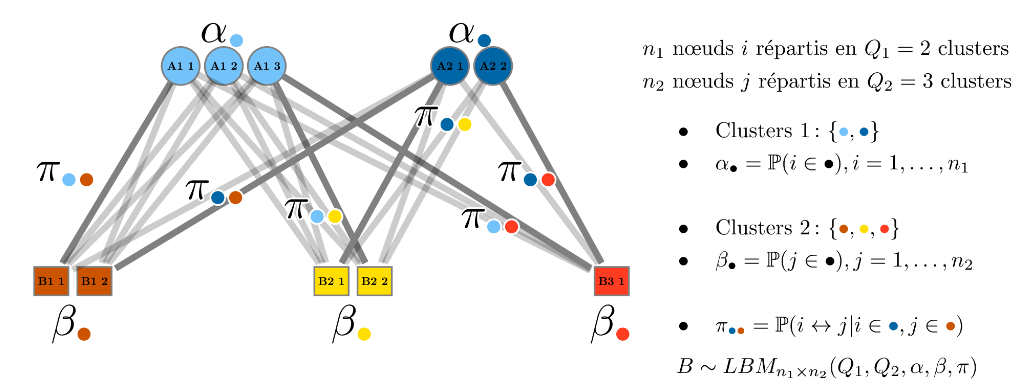
Latent block model
Probabilistic model for bipartite networks, credits to Louis Lacoste
\documentclass[border=3pt,tikz]{standalone}
\usepackage{pgfplots}
\usepackage[dvipsnames,table,xcdraw]{xcolor}
\usepackage{tikz}
\usepackage{amsmath}
\usepackage{amssymb}
\usepackage{enumitem}
\usepackage[outline]{contour} % glow around text
\contourlength{0.4pt}
\definecolor{electricblue}{rgb}{0.49, 0.98, 1.0}
\definecolor{cyanind}{rgb}{0.0, 0.4, 0.65}
\definecolor{blueind}{rgb}{0.45, 0.76, 0.98}
\definecolor{burntorange}{rgb}{0.8, 0.33, 0.0}
\definecolor{goldenyellow}{rgb}{1.0, 0.87, 0.0}
\definecolor{peach}{rgb}{1.0, 0.23, 0.13 }
\usetikzlibrary{arrows,automata}
\begin{document}
\begin{tikzpicture}[scale=0.35]
\tikzstyle{every state}=[draw, text=black,scale=0.95,
transform shape]
\tikzstyle{every state}=[draw=none,text=black,scale=0.75,
transform shape]
\tikzset{edge_proba/.style={draw=white, fill=none,
text=black}}
\tikzstyle{every node}=[fill=blueind]
\node[edge_proba] (pi1) at (1,5.7)
{\textbf{$\alpha_{{\color{blueind}\bullet}}$}};
\node[state, draw=black!50] (R11) at (0,5) {\textbf{A1 1}};
\node[state, draw=black!50] (R12) at (1,5) {\textbf{A1 2}};
\node[state, draw=black!50] (R13) at (2,5) {\textbf{A1 3}};
\tikzstyle{every node}=[fill=cyanind]
\node[edge_proba] (pi2) at (6.75,5.7)
{\textbf{$\alpha_{{\color{cyanind}\bullet}}$}};
\node[state, draw=black!50] (R21) at (6.25,5)
{\textbf{A2 1}};
\node[state, draw=black!50] (R22) at (7.25,5)
{\textbf{A2 2}};
% \tikzstyle{every node}=[fill=electricblue]
%\node[edge_proba] (pi3) at (10,5.7)
%{\textbf{$\alpha_{{\color{electricblue}\bullet}}$}};
%\node[state, draw=black!50] (R31) at (10,5) {\textbf{R31}};
\tikzstyle{every node}=[fill=burntorange, shape=rectangle]
\node[edge_proba] (pi3) at (-2.5,-1)
{\textbf{$\beta_{{\color{burntorange}\bullet}}$}};
\tikzstyle{every state}=[draw=none,text=black,scale=0.75,
transform shape, shape=rectangle]
\node[state, draw=black!50] (C11) at (-3,0) {\textbf{B1 1}};
\node[state, draw=black!50] (C12) at (-2,0) {\textbf{B1 2}};
\tikzstyle{every node}=[fill=goldenyellow, shape=rectangle]
\node[edge_proba] (pi3) at (4,-1)
{\textbf{$\beta_{{\color{goldenyellow}\bullet}}$}};
\node[state, draw=black!50] (C21) at (3.5,0) {\textbf{B2 1}};
\node[state, draw=black!50] (C22) at (4.5,0) {\textbf{B2 2}};
\tikzstyle{every node}=[fill=peach, shape=rectangle]
\node[edge_proba] (pi3) at (10,-1)
{\textbf{$\beta_{{\color{peach}\bullet}}$}};
\node[state, draw=black!50] (C31) at (10,0) {\textbf{B3 1}};
\tikzstyle{every edge}=[-,>=stealth',shorten
>=1pt,auto,draw,line width=1.5pt,draw opacity=0.2]
\path (R11) edge[-,>=stealth',shorten
>=1pt,auto,draw=gray,line width=1.5pt, fill=gray, opacity=1] node[midway, left,
fill=none] {\contour{white}{$\pi_{{\color{blueind}\bullet}{\color{burntorange}\bullet}}$}}
(C11);
\path (R11) edge (C12);
\path (R11) edge (C21);
\path (R11) edge (C22);
\path (R11) edge (C31);
\path (R12) edge (C31);
\path (R13) edge [-,>=stealth',shorten
>=1pt,auto,draw=gray,line width=1.5pt, fill=gray, opacity=1] node[pos = 0.75, right = -0.6cm,
fill=none] {\contour{white}{$\pi_{{\color{blueind}\bullet}{\color{peach}\bullet}}$}}(C31) ;
\path (R12) edge (C11);
\path (R12) edge (C12);
\path (R12) edge (C21);
\path (R12) edge (C22);
\path (R13) edge [] (C11);
\path (R13) edge (C12);
\path (R13) edge (C21);
\path (R13) edge[-,>=stealth',shorten
>=1pt,auto,draw=gray,line width=1.5pt, fill=gray, opacity=1] node[pos=0.7, right = -0.6cm,
fill=none] {\contour{white}{$\pi_{{\color{blueind}\bullet}{\color{goldenyellow}\bullet}}$}}
(C22);
\path (R21) edge (C22);
\path (R21) edge (C31);
\path (R22) edge (C21);
\path (R22) edge (C22);
\path (R21) edge[-,>=stealth',shorten
>=1pt,auto,draw=gray,line width=1.5pt, fill=gray, opacity=1] node[pos=0.2,
right = -0.2cm, fill=none]
{\contour{white}{$\pi_{{\color{cyanind}\bullet}{\color{goldenyellow}\bullet}}$}} (C21);
\path (R22) edge[-,>=stealth',shorten
>=1pt,auto,draw=gray,line width=1.5pt, fill=gray, opacity=1] node[midway, right = -0.6cm,
fill=none] {\contour{white}{$\pi_{{\color{cyanind}\bullet}{\color{peach}\bullet}}$}} (C31);
\path (R21) edge (C11);
\path (R21) edge[-,>=stealth',shorten
>=1pt,auto,draw=gray,line width=1.5pt, fill=gray, opacity=1] node[pos = 0.60, right = -0.6cm,
fill=none] {\contour{white}{$\pi_{{\color{cyanind}\bullet}{\color{burntorange}\bullet}}$}} (C12);
% \path (R31) edge[-,>=stealth',shorten
% >=1pt,auto,draw=gray,line width=1.5pt, fill=gray, opacity=1] node[midway,
% right, fill=none]
% {\contour{white}{$\pi_{{\color{electricblue}\bullet}{\color{peach}\bullet}}$}} (C31);
\tikzstyle{every node}=[fill=white, shape=rectangle,scale=0.5]
\node at (15,5) {
$ \begin{aligned}
& n_1 \text{ nœuds } i \text{ répartis en }Q_1=2 \text{ clusters}\\
& n_2 \text{ nœuds } j \text{ répartis en }Q_2=3 \text{ clusters}
\end{aligned}$
};
%\node at (15,4) {$n_2$ nœuds $i$ répartis en $Q_2=3$ clusters};
\node[below=1,align=center ] at (15,4) {$\begin{aligned}
& \bullet \quad \text{Clusters 1\,:}\ \{\textcolor{blueind}{\bullet},\textcolor{cyanind}{\bullet}\}\\
& \bullet \quad \alpha_{\bullet} = \mathbb{P}(i \in \bullet), i=1,\dots,n_1 \\
& \\
& \bullet \quad \text{Clusters 2\,:}\ \{\textcolor{burntorange}{\bullet},\textcolor{goldenyellow}{\bullet},\textcolor{peach}{\bullet}\}\\
& \bullet \quad \beta_{\bullet} = \mathbb{P}(j \in \bullet), j=1,\dots,n_2 \\
&\\
& \bullet \quad \pi_{\textcolor{cyanind}{\bullet}\textcolor{burntorange}{\bullet}} = \mathbb{P}(i
\leftrightarrow j | i\in\textcolor{cyanind}{\bullet},j\in\textcolor{burntorange}{\bullet})
\end{aligned}$
};
\node at (15,-2) {$B \sim LBM_{n_1\times n_2}(Q_1,Q_2,\alpha,\beta,\pi)$};
\end{tikzpicture}
\end{document}